![[BIG]](../icons/zoom18.gif){kind=icon}
![[Normal]](../icons/zoom14.gif){kind=icon}
![[small]](../icons/zoom10.gif){kind=icon}
Suiv.: Test 1: Problème thermique Sup.: 4 Tests conversationnels Préc.: 4 Tests conversationnels Table des matières
Suiv.: Test 1: Problème thermique
Sup.: 4 Tests conversationnels
Préc.: 4 Tests conversationnels
Table des matières
Cette section montre la façon de résoudre un problème en utilisant les programmes conversationnels de MODULEF.
On considère le problème aux limites suivant:
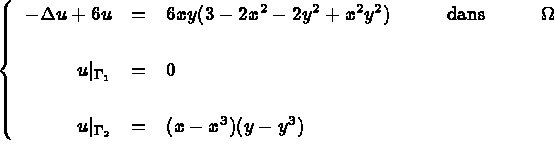
, et les frontières, 
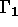et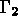 
, sont montrées sur la
figure 4.1
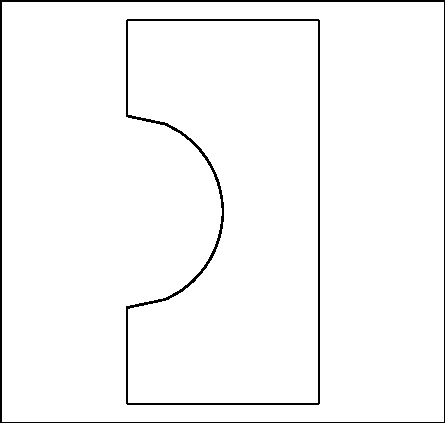
Figure 4.1: Exemple d'introduction
La solution exacte de ce problème est:
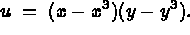
Nous résolvons ce problème en utilisant des éléments droits et courbes de degré 2 (éléments TRIA 2P2D et TRIA 2P2C de la bibliothèque THER).
En suivant les étapes vues en section 3.1.3, nous allons créer tous les fichiers de données nécessaires de manière interactive, exécuter les modules correspondants à ces étapes puis regarder la précision de la solution calculée en la comparant avec la solution exacte et, enfin, dessiner les isovaleurs de la solution.
Le préprocesseur APNOXX est utilisé pour construire le fichier de données et activer le mailleur 2D, APNOPO. Un appel de APNOXX produit un menu principal avec trois options:
Un fichier de données formaté est créé interactivement en sélectionnant l'option "CREATION du menu principal, i.e., en tapant la lettre "C" sur son clavier.
Rappel: Tapez en MAJUSCULES!
Apparaissent alors diverses questions et impressions, auxquels vous devez répondre en tapant le mot-clé approprié, la valeur demandée, etc. On définit, via IMPRE, le taux des impressions qui apparaîtront à l'écran lors de l'exécution du module (par exemple pour aider à une recherche d'erreur), cette valeur varie de 0 à 10, 0 indique que l'on ne veut pas d'impression lors de l'exécution, 10 indique que l'on veut le maximum d'impressions lors de cette exécution. En répondant "O" (OUI) à l'option " DES DETAILS ", on obtiendra quelques conseils. Les réponses fournies seront indiquées entre parenthèses dans ce qui suit.
Le processus complet, création des fichiers, exécution et résultats, est joint pour chaque étape afin de vous familiariser avec le monde MODULEF (vocabulaire, modules, abréviations, etc.).
Voici l'exemple complet relatif au problème considéré:
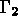est définie par une fonction interprétée, i.e., répondre
" O " à la question
Des conseils sont donnés si on tape " ? ".
Les premières valeurs à fournir sont:
IMPRE 10), et
Une courbe est définie par un nombre (entre 1 et 99) qui sera associé à chaque équation de courbes. Ce numéro servira quand le numéro de référence d'une ligne ou d'une arête (pour les mots-clés LIGN et RETR, respectivement) sera rencontré. Ici, la courbe est identifiée par le numéro de référence 2, tandis que la ligne droite l'est par le numéro 1.
Chaque courbe doit être définie comme suit:
|
|
Comme ci-dessus, on a d'abord:
Chaque ligne est définie en donnant:
si NFFRON = 0 la ligne est la ligne droite joignant NEXTR1 à NEXTR2
(ex: NFFRON = 0 pour les lignes 1, 2, 3, 4, et 6), ou
si NFFRON = -1 les points intermédiaires sont donnés à la main, ou
si NFFRON = -2 , la ligne est la portion du cercle centré à l'origine
et passant par les points NEXTR1 et NEXTR2, ou
si NFFRON = -3 , la ligne est la portion du cercle centré au point de numéro
donné et passant par les points NEXTR1 et NEXTR2.
Note: En tapant " O " à la question " DES DETAILS ", on a ces indications à l'écran.
POIN et LIGN ont dû être appelés avant.
Les 4 côtés du quadrangle sont définis par:
|
|
Note: Le nombre de points doit être égal sur les côtés opposés.
On donne ensuite:
La liste des lignes formant le contour est donnée comme suit:
Enfin, on indique:
Il ne peut être activé qu'après les précédents.
On donne:
Il vient à la fin du processus, juste avant SAUV et FIN.
On donne:
On peut l'activer à tout moment pour sauver tout ou partie du maillage.
On doit fournir:
Quand le fichier de données a été créé, on est prêt pour construire le maillage tel qu'il est décrit dans ce fichier. Il suffit de choisir l'option EXECUTION du menu principal.
Les données sont alors:
En fonction du paramètre IMPRE choisi, plus ou moins d'impressions vont apparaître à l'écran. Une fois l'exécution terminée, on retourne dans le menu principal dont on sort en tapant " FIN ".
On donne maintenant l'image de ce qui apparaît à l'écran pour ce processus:
B$ apnoxx
***************
APPEL DE APNOPO : ( MAILLAGE 2D )
***************
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
C
-- TITRE DU TRAVAIL ( 20 CARACTERES AU PLUS ) ?
'TEST EXAMPLE'
*******************************************************************************
CREATION CONVERSATIONNELLE DES DONNEES DE APNOPO
*******************************************************************************
** ECRIRE EN MAJUSCULES S.V.P.
-- NOM DU FICHIER DE COMMANDES A CREER (A) ?
NOPO.DATA
-- HELP (OUI-NON) ?
N
-- UTILISER LES FONCTIONS INTERPRETEES (OUI-NON-?) ?
O
-- DES DETAILS (OUI-NON) ?
N
-- IMPRE NFONC ?
1 1
LES 1 COURBES SONT NUMEROTEES DE 1 A 1 (OUI-NON) ?
N
** DONNER L'EXPRESSION F(X,Y) ( = 0. ) EN FINISSANT PAR ;
** LONGUEUR MAXI A64 ( 64 ESPACES )
** EXEMPLE :' X**2 + Y**2 - 4;'
OU : X*X+Y*Y-4;
NUMERO DE LA COURBE 1 ?
2
-- COURBE 1 DE NUMERO 2 :
X**2+Y**2-0.25;
-- MOT CLEF ?
POIN
-- DES DETAILS (OUI-NON) ?
N
-- IMPRE NPOINT ?
1 6
-- POINT NUMERO 1 : NOREF X Y ?
1 0 -1
-- POINT NUMERO 2 : NOREF X Y ?
1 1 -1
-- POINT NUMERO 3 : NOREF X Y ?
1 1 1
-- POINT NUMERO 4 : NOREF X Y ?
1 0 1
-- POINT NUMERO 5 : NOREF X Y ?
1 0 0.5
-- POINT NUMERO 6 : NOREF X Y ?
1 0 -0.5
-- RESTER DANS CE MOT-CLE (OUI-NON) ?
N
-- MOT CLEF ?
LIGN
-- DES DETAILS (OUI-NON) ?
N
-- IMPRE NDLM ?
1 6
-- LIGNE NUMERO 1 : NOELIG NEXTR1 NEXTR2 NOREFL NFFRON RAISON ?
5 1 2 1 0 1
-- LIGNE NUMERO 2 : NOELIG NEXTR1 NEXTR2 NOREFL NFFRON RAISON ?
10 2 3 1 0 1
-- LIGNE NUMERO 3 : NOELIG NEXTR1 NEXTR2 NOREFL NFFRON RAISON ?
5 3 4 1 0 1
-- LIGNE NUMERO 4 : NOELIG NEXTR1 NEXTR2 NOREFL NFFRON RAISON ?
3 4 5 1 0 1
-- LIGNE NUMERO 5 : NOELIG NEXTR1 NEXTR2 NOREFL NFFRON RAISON ?
6 6 5 2 10 1
** LA FONCTION D'INDICE 2 DECRIRA LA LIGNE 5
-- LIGNE NUMERO 6 : NOELIG NEXTR1 NEXTR2 NOREFL NFFRON RAISON ?
3 6 1 1 0 1
-- RESTER DANS CE MOT-CLE (OUI-NON) ?
N
-- MOT CLEF ?
QUAC
-- DES DETAILS (OUI-NON) ?
N
-- IMPRE NIVEAU NUDSD NBRELI NS1L ?
1 1 1 6 1
-- NOLO( 1) ?
1
-- NOLO( 2) ?
2
-- NOLO( 3) ?
3
-- NOLO( 4) ?
4
-- NOLO( 5) ?
5
-- NOLO( 6) ?
6
-- IMAX NQUAD ?
5 -1
-- ANNULER (OUI-NON) ?
N
-- MOT CLEF ?
ADPO
-- DES DETAILS (OUI-NON) ?
N
-- IMPRE NIVEA1 NIVEA2 N1 ISET ISEQ NOESOM ?
1 1 2 1 0 0 1
-- ANNULER (OUI-NON) ?
N
-- MOT CLEF ?
RENC
-- DES DETAILS (OUI-NON) ?
N
-- IMPRE NIVEA1 NIVEA2 ?
1 2 1
-- ANNULER (OUI-NON) ?
N
-- MOT CLEF ?
SAUV
-- DES DETAILS (OUI-NON) ?
N
-- IMPRE NINOPO NOM_NOPO NTNOPO ?
1 1 TEST.NOPO 0
-- ANNULER (OUI-NON) ?
N
-- MOT CLEF ?
FIN
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
E
-- NOM DU FICHIER DE COMMANDES ?
NOPO.DATA
------------------------------------------------------------------------------
COURBES
------------------------------------------------------------------------------
** TRAITEMENT DU MOT CLE COUR
------------------------------
++ OPEN(11,FILE='',SPEC='SCRATCH,UNFORMATTED',RECL=0)
------------------------------------------------------------------------------
POIN
------------------------------------------------------------------------------
** TRAITEMENT DU MOT CLE POIN
------------------------------
------------------------------------------------------------------------------
LIGN
------------------------------------------------------------------------------
** TRAITEMENT DU MOT CLE LIGN
------------------------------
------------------------------------------------------------------------------
QUAC
------------------------------------------------------------------------------
** TRAITEMENT DU MOT CLE QUAC
------------------------------
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE QUACOO : TEST EXAMPLE
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
FIN DU MODULE QUACOO
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
------------------------------------------------------------------------------
ADPO
------------------------------------------------------------------------------
** TRAITEMENT DU MOT CLE ADPO
------------------------------
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE ADPNOP : TEST EXAMPLE
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
FIN DU MODULE ADPNOP
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
------------------------------------------------------------------------------
RENC
------------------------------------------------------------------------------
** TRAITEMENT DU MOT CLE RENC
------------------------------
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE GIBBS : TEST EXAMPLE
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE RENUM1 : TEST EXAMPLE
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
RENUMEROTATION DES NOEUDS
-------------------------
NOMBRE DE NOEUDS : 171
------------------------------------------------------------------
I CARACTERISTIQUES I AVANT RENUMEROTATION I APRES RENUMEROTATION I
------------------------------------------------------------------
I LARGEUR DE BANDE I 133 I 30 I
------------------------------------------------------------------
I PROFIL TOTAL I 11718 I 1998 I
I PROFIL MOYEN I 68.526 I 11.684 I
------------------------------------------------------------------
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
FIN DU MODULE RENUM1
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
FIN DU MODULE GIBBS
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
------------------------------------------------------------------------------
SAUV
------------------------------------------------------------------------------
** TRAITEMENT DU MOT CLE SAUV
------------------------------
++ OPEN(12,FILE='test.nopo',SPEC='UNFORMATTED',RECL=0)
------------------------------------------------------------------------------
FIN
------------------------------------------------------------------------------
** TRAITEMENT DU MOT CLE FIN
------------------------------
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
FIN DU MODULE APNOPO
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
FIN
Le fichier de données construit a la forme suivante:
'TEST EXAMPLE '
COURBES
1 $ IMPRE
COURBE02(X,Y)=
X**2+Y**2-0.25;
FIN
'POIN '
1 6 $ IMPRE NPOINT $
$ NOP NOREF(NOP) X(NOP). Y(NOP). $
1 1 0.000000E+00 -.100000E+01
2 1 0.100000E+01 -.100000E+01
3 1 0.100000E+01 0.100000E+01
4 1 0.000000E+00 0.100000E+01
5 1 0.000000E+00 0.500000E+00
6 1 0.000000E+00 -.500000E+00
'LIGN '
1 6 $ IMPRE NDLM $
$ NOLIG NOELIG NEXTR1 NEXTR2 NOREFL NFFRON RAISON $
1 5 1 2 1 0 0.100000E+01
2 10 2 3 1 0 0.100000E+01
3 5 3 4 1 0 0.100000E+01
4 3 4 5 1 0 0.100000E+01
5 6 6 5 2 10 0.100000E+01
6 3 6 1 1 0 0.100000E+01
'QUAC '
1 1 1 6 1 $ IMPRE NIVEAU NUDSD NBRELI NS1L
$ LISTE DES LIGNES DU CONTOUR :
1 2 3 4 5 6
5 -1 $ IMAX NQUAD
'ADPO '
1 1 2 1 0 $ IMPRE NIVEA1 NIVEA2 N1 ISET
0 1 $ ISEQ NOESOM
'RENC '
1 2 1 $ IMPRE NIVEA1 NIVEA2
'SAUV '
1 1 0 $ IMPRE NINOPO NTNOPO
TEST.NOPO
$ NOM FICHIER
'FIN '
Le maillage résultat est stocké dans une structure de données, dont vous avez défini le nom dans le fichier de données, il peut être affiché en utilisant le préprocesseur TRNOXX, en indiquant ce nom:
| Appeler le préprocesseur: | TRNOXX | |
| Taper le nom du fichier contenant la structure: | TEST.NOPO |
La figure 4.2 montre ce maillage.
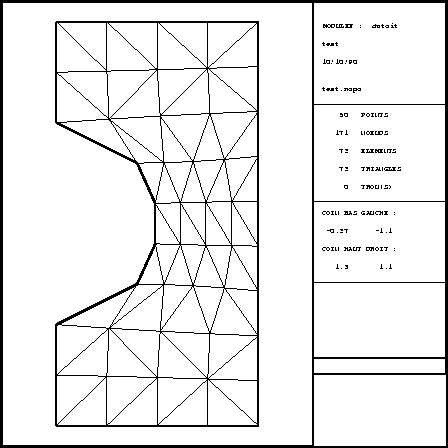
Figure: Le maillage (dessin dû à TRNOXX)
On peut maintenant, disposant du maillage, la S.D. NOPO, passer à l'étape suivante.
A partir de la S.D. NOPO, maintenant disponible, on va définir l'interpolation. L'exemple traité est un problème de type thermique. On va donc choisir le (les) élément(s) fini(s) dans la bibliothèque THERMIQUE. Etant en dimension 2, nous décidons d'utiliser les triangles (TRIA) droits et courbes dont les polynômes de base sont de degré 2 (P2 Lagrange), de noms TRIA 2P2D et TRIA 2P2C dans le code MODULEF.
Le préprocesseur COMAXX permet de réaliser cette opération. Comme pour l'étape 1, un fichier de données est construit en prenant l'option CREATION du menu principal, et en répondant aux différentes questions.
Ces données sont décrites en détails ci-dessous:
La donnée des courbes se fait de la même façon qu'à l'étape 1.
La liste des bibliothèques disponibles peut être obtenue en tapant " ? " comme réponse à la question " NOM DE LA BIBLIOTHEQUE ? ".
Taper " ? " en cas de doute.
Le fichier de données étant construit, on exécute le module en prenant l'option EXECUTION du menu principal.
Les valeurs à fournir sont alors:
IMPRE 10) (ex: 5).
Suit le listing de la session:
B$ comaxx
***************
APPEL DE COMACO : ( INTERPOLATION )
***************
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
C
*******************************************************************************
CREATION CONVERSATIONNELLE DES DONNEES DE COMACO
*******************************************************************************
-- NOM DU FICHIER DE COMMANDES A CREER ?
COMA.DATA
-- DIMENSION DE L' ESPACE ?
2
-- UTILISER LES FONCTIONS INTERPRETEES (OUI-NON-?) ?
O
PARAMETRE D' IMPRESSION (I) IMPRE
NOMBRE DE COURBES A DEFINIR (I) NFONC
-- IMPRE NFONC ?
1 1
LES 1 COURBES SONT NUMEROTEES DE 1 A 1 (OUI-NON) ?
N
** DONNER L'EXPRESSION F(X,Y) ( = 0. ) EN FINISSANT PAR ;
** LONGUEUR MAXI A64 ( 64 ESPACES )
** EXEMPLE :' X**2 + Y**2 - 4;'
OU : X*X+Y*Y-4;
NUMERO DE LA COURBE 1 ?
2
-- COURBE 1 DE NUMERO 2 :
X**2+Y**2-0.25;
-- NOMBRE DE SOUS-DOMAINES ?
1
-- NOMBRE DE NUMEROS DE REFERENCE ?
2
-- NOMBRE DE LIGNES COURBES ?
1
-- NUMERO DE LA LIGNE COURBE : 1 ?
2
** APPEL DE LA BIBLIOTHEQUE D ELEMENTS ( IDTECA=0 ) **
-- NOM DE LA BIBLIOTHEQUE ( NOM EN A4 OU ? ) ?
THER
-- NOMBRE DE TYPES D ELEMENTS DROITS DU SOUS-DOMAINE : 1 ?
1
-- NOM DE L' ELEMENT ( EN A4,1X,A4 OU ? ) DROIT ?
TRIA 2P2D
-- NOMBRE DE TYPES D ELEMENTS COURBES DU SOUS-DOMAINE : 1 ?
1
-- NOM DE L' ELEMENT ( EN A4,1X,A4 OU ? ) COURBE ?
TRIA 2P2C
-- NOM DU FICHIER DE LA S.D.E. NOPO ?
TEST.NOPO
-- NOM DU FICHIER DE LA S.D.S. MAIL ?
TEST.MAIL
-- NOM DU FICHIER DE LA S.D.S. COOR ?
TEST.COOR
-- Y A T'IL DES TABLEAUX A ASSOCIER (OUI-NON) ?
N
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
E
-- NOM DU FICHIER CONTENANT LES DONNEES ?
COMA.DATA
-- PARAMETRE D'IMPRESSION DES S.D. ?
1
++ OPEN(11,FILE='test.nopo',SPEC='OLD,UNFORMATTED',RECL=0)
++ OPEN(12,FILE='test.mail',SPEC='UNFORMATTED',RECL=0)
++ OPEN(13,FILE='test.coor',SPEC='UNFORMATTED',RECL=0)
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE COMACO :
FIN DU MODULE COMACO
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
TABLEAU M A I 2
----------------
DIMENSION DE L'ESPACE (NDIM) : 2
NOMBRE D'INCONNUES DE LA FORMULATION VARIATIONNELLE (NINCFV) : 1
NOMBRE DE TYPES D'ELEMENTS (NTYELM) : 2
NOMBRE DE NUMEROS DE REFERENCES (NNR) : 2
NOMBRE DE TYPES DE NOEUDS (NTYNOE) : 1
NOMBRE DE TYPES DE POINTS (NTYPOI) : 1
NOMBRE DE MOTS DU TABLEAU MAI3 (LMAI3) : 36
LES POINTS NE SONT DEFINIS QUE PAR LEURS COORDONNEES
NOEUDS ET POINTS NE COINCIDENT PAS PARTOUT (NCO) : 0
NOMBRE MAXIMUM DE MOTS POUR UN ELEMENT (NMMAEL) : 28
NOMBRE DE MOTS DU TABLEAU MAIL (LMAIL) : 1421
OPTION DE STOCKAGE (NOPFI) : 0
TABLEAU C O O 2
---------------
TYPE DU TABLEAU COO4 (NTYT) : 2
NOMBRE DE SES INDICES (NINDI) : 2
DIMENSION DU DOMAINE (NDIM) : 2
VALEUR MAXIMALE DU DEUXIEME INDICE (M2) : 65
CODE DE LA SEGMENTATION (NCODS) : 1
NOMBRE DE BLOCS (NBLOC) : 1
TYPE DES AXES DES COORDONNEES (NTACOO) : 1
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
F
Le fichier de données étant:
1 $ Y A T IL DES FONCTIONS INTERPRETEES
1 $ IMPRE
COURBE02(X,Y)=
X**2+Y**2-0.25;
FIN
2 1 0 $ NDIM NDSD NBSDC
2 1 $ NNR NBLC
2
THER $ NOM DE LA BIBLIOTHEQUE
1 $ NTYED DU SD 1
TRIA 2P2D $ LE NOM DES ELEMENTS DROITS
1 $ NTYEC DU SD 1
TRIA 2P2C $ LE NOM DES ELEMENTS COURBES
TEST.NOPO $ NOM DU FICHIER
0 $ ET NIVEAU DE LA SD NOPO
TEST.MAIL $ NOM DU FICHIER
0 $ ET NIVEAU DE LA SD MAIL
TEST.COOR $ NOM DU FICHIER
0 $ ET NIVEAU DE LA SD COOR
0 0 $ NTMAIL NTCOOR
Le maillage étant construit et l'interpolation étant définie, on peut passer au calcul des tableaux élémentaires. Il est donc nécessaire de fournir les données physiques du problème. Comme déjà vu à la section 3.1.2, cet exemple est un cas particulier du problème thermique classique qui revient à fixer correctement les paramètres demandés. C'est-à-dire que, si:
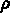
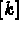
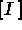, la 
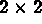matrice unité,
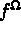
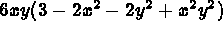, et
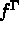
La description des données est faite via le préprocesseur FOMIXX. On choisit de définir la fonction
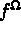par la subroutine FORCEV (imprimée ci-dessous) et le reste des données 
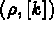par le tableau /CAR.
Les données à taper sont décrites ci-dessous:
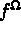). Le nombre de cas de charge, ou seconds membres, est donné par:
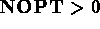pour un matériau isotrope, et 
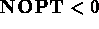sinon.
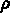et [k] pour calculer la
matrice de masse et celle de rigidité).
Dans notre exemple, pour les calculs (équations (3.7) et (3.8)), on a besoin de:
:
:
.
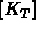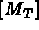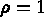Si des données sont inutiles pour le problème posé, par
exemple g et 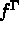sont nuls, on peut ne pas les fournir.
Ici, donc, on tape simplement:
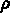(ex: 1),
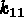(ex: 1),
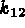(ex: 0), et
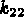(ex: 1).
Un commentaire, écrit entre apostrophes, doit être entré pour finir de décrire le tableau
En cas d'erreur, on peut recommencer la saisie du tableau en cours de traitement.
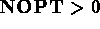cas isotrope, et 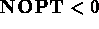sinon.
Le fichier de données est maintenant créé, on se retrouve dans le menu principal, on peut alors choisir de créer un autre fichier de données par l'option (C), exécuter le module via l'option (E) ou terminer la session par l'option (FIN). Supposons que l'on choisisse de taper " E " pour exécuter FOMIXX, les données sont alors:
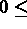IMPRE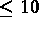 
) (ex: 5).
Suit le listing de la session:
B$ fomixx
*************************
APPEL DE COFORC ET COMILI : ( DONNEES )
*************************
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
C
****************************************
CREATION DES DONNEES DE COFORC ET COMILI
****************************************
-- NOM DU FICHIER A CREER (A) ?
FOMI.DATA
-- DES DETAILS (OUI-NON) ?
N
-- NOMFIC (FORC) NIFORC NTFORC ?
TEST.FORC 1 0
-- NOMFIC (MILI) NIMILI NTMILI ?
TEST.MILI 1 1
** ON VA DECRIRE LA MANIERE DONT SERONT FOURNIES LES DONNEES
NECESSAIRES AU CALCUL DU (DES) SECOND(S) MEMBRE(S)
-- NDSM ?
1
-- TRAITEMENT PAR LOT ( NUMEROS DE SD OU REFERENCE ) (OUI-NON) ?
O
-- NDIM NDSD NBFR ?
2 1 0
DONNEES SURFACIQUES S-D : 1 (OUI-NON) ?
O
AUTRES INFORMATIONS (OUI-NON) ?
N
-- NOPT ITRAIT ( SURFACE REFERENCE : 1 ) ?
1 2
-- LOPT IADR ?
1 1
** DESCRIPTION DES DONNEES POUR LA(LES) MATRICE(S)
NOMBRE DE TABLEAUX ASSOCIES A LA S.D. MILI : 1
POUR CHAQUE TABLEAU DECRIT :
SON NOM (A) NOMTAB
SON TYPE ( 1 A 6 ) (I) NTYTAB
** ENTIER 1 , SP 2 , DP 5 , LOGIQUE 3 , CHARACTER 4...
** EN THERMIQUE : SIMPLE PRECISION => TYPE 2
** EN ELASTICITE : DOUBLE PRECISION => TYPE 5
SON NOMBRE DE VARIABLES (I) NBVAR
** TABLEAU 1 ASSOCIE A LA S.D. MILI
-- NOMTAB NTYTAB NBVAR ?
/CAR 2 4
** LES VARIABLES DU TABLEAU /CAR
-- /CAR( 1) = ?
1
-- /CAR( 2) = ?
1
-- /CAR( 3) = ?
0
-- /CAR( 4) = ?
1
** COMMENTAIRES SUR LE TABLEAU /CAR
(60 CARACTERES MAXI ENTRE ')
'RO ET K (MATRICE UNITE)'
-- REDONNER LES CARACTERISTIQUES DE CE TABLEAU :/CAR (OUI-NON) ?
N
-- TRAITEMENT PAR LOT ( NUMEROS DE SD OU REFERENCE ) (OUI-NON) ?
OUI
-- NDIM NDSD NBFR ?
2 1 0
DONNEES SURFACIQUES S-D : 1 (OUI-NON) ?
O
AUTRES INFORMATIONS (OUI-NON) ?
N
-- NOPT ITRAIT ( SURFACE REFERENCE : 1 ) ?
1 1
-- NTABL IADR ?
/CAR 1
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
E
-- NOM DU FICHIER CONTENANT LES DONNEES (A) ?
FOMI.DATA
-- PARAMETRE D'IMPRESSION DES SD ?
1
++ OPEN(11,FILE='test.forc',SPEC='UNFORMATTED',RECL=0)
++ OPEN(12,FILE='test.mili',SPEC='UNFORMATTED',RECL=0)
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE COFORC :
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
FIN DU MODULE COFORC
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE COMILI :
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
FIN DU MODULE COMILI
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
TABLEAU F O R 2
----------------
PRESENCE ( NOMBRE DE GROUPES ) OU ABSENCE ( 0 ) DE RENSE IGNEMENT
--------------------------------------------------
| | | |
| | SOUS-DOMAINES | ELEMENTS |
| | | |
--------------------------------------------------
| VOLUMES | 0 | 0 |
| SURFACES | 1 | 0 |
| LIGNES | 0 | 0 |
| POINTS | 0 | 0 |
--------------------------------------------------
TABLEAU M I L 2
----------------
PRESENCE ( NOMBRE DE GROUPES ) OU ABSENCE ( 0 ) DE RENSEIGNEMENT
--------------------------------------------------
| | | |
| | SOUS-DOMAINES | ELEMENTS |
| | | |
--------------------------------------------------
| VOLUMES | 0 | 0 |
| SURFACES | 1 | 0 |
| LIGNES | 0 | 0 |
| POINTS | 0 | 0 |
--------------------------------------------------
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
FIN
Le fichier de données construit par le préprocesseur FOMIXX est le suivant:
' '
TEST.FORC $ NOM DU FICHIER DE LA S.D FORC
1 0 $ SON NIVEAU ET NB DE SES TAB. ASSOCIES
TEST.MILI $ NOM DU FICHIER DE LA S.D MILI
1 1 $ SON NIVEAU ET NB DE SES TAB. ASSOCIES
$ DONNEES RELATIVES A LA S.D. FORC $
1 $ NDSM
0 1 0 0 0 0 0 0
1 0 1 2 $ NOSD NFRO NOPT ITRAIT
1 1 $ LOPT IADR
$ DONNEES RELATIVES A LA S.D. MILI $
/CAR 2 4 $ NOM TYPE NBREMOT
0.100000E+01 $ /CAR( 1)
0.100000E+01 $ /CAR( 2)
0.000000E+00 $ /CAR( 3)
0.100000E+01 $ /CAR( 4)
' RO ET K (MATRICE UNITE) ' $ CONTENU
0 1 0 0 0 0 0 0
1 0 1 1 $ NOSD NFRO NOPT ITRAIT
/CAR 1 $ NTABL IADR
La subroutine FORCEV correspondant à l'exemple est la suivante:
SUBROUTINE FORCEV(M,LOPT,X,NDIM,NPO,TAR,LTAR,LVECT,IADR,I1,
& NARE,IA)
C.....................................................................
C AIM:
C INPUT THE HEAT QUANTITIES IN ORDER TO CALCULATE THE
C ELEMENT RHS VECTORS FOR A THERMAL PROBLEM.
C.....................................................................
C INPUT PARAMETERS:
C M SUPER ARRAY
C LOPT COFORC PARAMETER
C X ELEMENT COORDINATE TABLE
C NDIM DIMENSION
C NPO NUMBER OF POINTS FOR THE ELEMENT
C LTAR NUMBER OF WORDS OF THE ARRAY TAR FOR EVERY ELEMENT
C LVECT NUMBER OF SAME COLOR ELEMENTS
C IADR COFORC PARAMETER
C I1 0 USUALLY (SEE DOC 14)
C NARE FACE NUMBER (3D), EDGE NUMBER (2D)
C IA ADRESS -1 IN MAIL OF THE 1ST WORD OF THE CURRENT ELEMENT
C
C OUTPUT PARAMETERS:
C TAR ARRAY TAR(LTAR,LVECT)
C......................................................................
C
INTEGER M(*), NDIM,NPO,LTAR,LVECT,IADR,I1,NARE,IA,LOPT
REAL X(NPO,NDIM),TAR(*)
C
INTEGER IP(3)
DATA IP/2,3,1/
C
IF (NPO .EQ. 3) THEN
C
C THE ELEMENT IS STRAIGHT
C
DO 1 I = 1, 3
XM = 0.5*(X(I,1)+X(IP(I),1))
YM = 0.5*(X(I,2)+X(IP(I),2))
TAR(I) = 6*XM*YM*(3-2*(XM**2)-2*(YM**2)+(XM**2)*(YM**2))
1 CONTINUE
ELSE IF (NPO.EQ. 6) THEN
C
C THE ELEMENT IS CURVED
C
DO 2 I = 1, 6
TAR(I) = 6*X(I,1)*X(I,2)*(3-2*X(I,1)**2-2*X(I,2)**2
+ +X(I,1)**2*X(I,2)**2)
2 CONTINUE
ELSE
C
C ERROR MESSAGE
C
IMPRIM = IINFO('I')
WRITE(IMPRIM,1000) 'ERROR FORCE'
STOP
END IF
1000 FORMAT(1X,A)
END
Commentaire: Les deux types d'éléments finis n'ont pas nécessairement le même nombre de données. Il est possible de distinguer un élément droit et un élément courbe par le nombre de leurs points (3 dans le premier cas et 6 pour l'élément courbe).
Les tableaux élémentaires sont créés par le préprocesseur THELXX. On construit d'abord un fichier de données en prenant l'option CREATION du menu principal et en fournissant les valeurs demandées.
C'est-à-dire:
Il y a une combinaison linéaire à faire entre la masse et la rigidité (ex : " O " et 1). Ses coefficients sont stockés dans un tableau, /LIN dans notre exemple, qui contient les valeurs (6, 1) (revoir la formulation variationnelle du problème).
Maintenant que le fichier de données est prêt, on peut choisir l'option
[4] EXECUTION du
menu principal. Cependant, avant de pouvoir lancer l'exécution de THELXX, la subroutine
FORCEV doit être compilée et liée au préprocesseur THELXX.
Les données pour l'exécution sont:
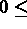IMPRE 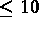) (ex: 5).
La session est reproduite ci-dessous:
B$ thelxx
***************
APPEL DE THELAS (NEW): ( CALCULS ELEMENTAIRES )
***************
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
C
*******************************************************************************
CREATION CONVERSATIONNELLE DES DONNEES DE THELAS
*******************************************************************************
-- NOM DU FICHIER A CREER ?
TAE.DATA
-- NOM DU FICHIER DE LA S.D.E. MAIL ?
TEST.MAIL
-- NOM DU FICHIER DE LA S.D.E. COOR ?
TEST.COOR
-- NOM DU FICHIER DE LA S.D.S. TAE ?
TEST.TAE
-- Y A T'IL DES TABLEAUX A ASSOCIER (OUI-NON) ?
N
-- UTILISEZ-VOUS LE FICHIER POBA (OUI-NON) ?
( POLYNOMES DE BASE ... EN ACCES DIRECT )
N
-- UTILISEZ-VOUS LA S.D. MILI (OUI-NON) ?
OUI
-- NOM DU FICHIER DE LA S.D.E. MILI ?
TEST.MILI
-- UTILISEZ-VOUS LA S.D. FORC (OUI-NON) ?
O
-- NOM DU FICHIER DE LA S.D.E. FORC ?
TEST.FORC
-- PROVENANCE DU PROBLEME (NPROV) ?
1 : THERMIQUE , 2 : ELASTICITE , 3 : LIGNES DE COURANT
1
-- CALCUL DE LA MATRICE DE MASSE (OUI-NON) ?
O
-- ELLE PEUT ETRE DIAGONALE (OUI-NON) ?
N
-- CALCUL DE LA MATRICE DE RAIDEUR (OUI-NON) ?
O
-- CALCUL DU OU DES SECONDS MEMBRES (OUI-NON) ?
O
-- CALCUL DU FLUX (OUI-NON) ?
N
-- Y A T'IL DES COMBINAISONS LINEAIRES MASSE-RAIDEUR (OUI-NON) ?
O
-- NOMBRE DE COMBINAISONS LINEAIRES MASSE-RAIDEUR ?
1
-- NOM (4 CARACTERES ) DU TABLEAU DE CES VALEURS ?
/LIN
-- COEFFICIENTS DE LA COMBINAISON NUMERO : 1 ?
6 1
-- NOM DU TABLEAU DES COULEURS (NOMCOU) OU VIDE
ET LONG MAX DES VECTEURS (LVECT)
VIDE 1
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
E
!! VOUS UTILISEZ LA NOUVELLE VERSION DE THELAS
VOTRE FICHIER DE DONNEES DOIT SE TERMINER PAR :
VIDE 1 $ NOMCOU LVECT
-- NOM DU FICHIER CONTENANT LES DONNEES ?
TAE.DATA
-- PARAMETRE D'IMPRESSION DE LA SD ?
1
++ OPEN(11,FILE='test.mail',SPEC='OLD,UNFORMATTED',RECL=0)
++ OPEN(12,FILE='test.coor',SPEC='OLD,UNFORMATTED',RECL=0)
++ OPEN(13,FILE='test.tae',SPEC='UNFORMATTED',RECL=0)
++ OPEN(14,FILE='test.mili',SPEC='OLD,UNFORMATTED',RECL=0)
++ OPEN(15,FILE='test.forc',SPEC='OLD,UNFORMATTED',RECL=0)
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE THENEW :
** WARNING READRE : TABLEAU TRAV DE LONGUEUR NULLE SON ADRESSE EST MISE A 1
TABLEAU T A E 2
----------------
NOMBRE D'ELEMENTS (NE) : 72
NOMBRE DE NOEUDS (NOE) : 171
NOMBRE DE TABLEAUX ASSOCIES A CHAQUE ELEMENT (NTACE) : 2
NOMBRE MAXIMUM DE NOEUDS D'UN ELEMENT (NNOMAX) : 6
NOMBRE CONSTANT DE D.L. PAR NOEUD ( 0 SI NON ) (ND) : 1
NOMBRE MAXIMUM DE D.L. PAR NOEUD (NDLMAX) : 1
NOMBRE DE TYPE D'ELEMENTS (NTYELM) : 2
SOMME DU NOMBRE DE NOEUDS DES TYPES D'ELEMENTS (LNOET) : 12
PROBLEME : 1 THERMIQUE, 2 ELASTIQUE, 3 AUTRE (NPROV) : 1
LES OPTIONS CHOISIES (NOPTNT) : 0
NUMERO DU TABLEAU ASSOCIE QUI REPRESENTE :
LA MASSE : 0
LA RAIDEUR : 0
LA PREMIERE COMBINAISON LINEAIRE : 1
LA DERNIERE : 1
LE(S) SECOND(S) MEMBRE(S) : 2
LES CONTRAINTES OU LE FLUX : 0
FIN DU MODULE THENEW
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
FIN
Le fichier de données est le suivant:
TEST.MAIL $ NOM DU FICHIER
1 $ ET NIVEAU DE LA SD MAIL
TEST.COOR $ NOM DU FICHIER
1 $ ET NIVEAU DE LA SD COOR
TEST.TAE $ NOM DU FICHIER
1 $ ET NIVEAU DE LA SD TAE
0 $ NTTAE
0 $ 1 SI POBA EST UTILISEE , 0 SINON
1 $ 1 SI MILI EST UTILISEE , 0 SINON
TEST.MILI $ NOM DU FICHIER
1 $ ET NIVEAU DE LA SD MILI
1 $ 1 SI FORC EST UTILISEE , 0 SINON
TEST.FORC $ NOM DU FICHIER
1 $ ET NIVEAU DE LA SD FORC
1 $ NPROV
1 1 1 0 $ IOPT(*)
/LIN 1 $ NOM DU TABLEAU DES CL ET NOMBRE DE CL
0.6000000E+01 0.1000000E+01 $ COEFFICIENTS DES CL
VIDE 1 $ NOMCOU LVECT
Le traitement des conditions aux limites imposées est le rôle du préprocesseur COBDXX. Le fichier de données est créé en prenant l'option CREATION du menu principal.
Les données sont décrites ci-dessous:
le type de ces valeurs (ex: 2)
2: simple précision, ou
5: double précision.
Ici, on a donc:
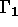: u = 0 (ex: 0;), et
: 
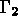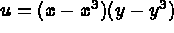
On peut maintenant exécuter (E) COBDXX, ensuite, on sort de la session en tapant "FIN ".
Les données pour cette exécution sont:
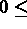IMPRE 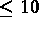) (ex: 5).
On montre la session obtenue par appel de ce préprocesseur COBDXX:
B$ cobdxx
***************
APPEL DE COBDC1 : ( CONDITIONS LIMITES )
***************
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
C
*******************************************************************************
CREATION CONVERSATIONNELLE DES DONNEES DE COBDC1
*******************************************************************************
-- NOM DU FICHIER A CREER ?
BDCL.DATA
-- NOM DU FICHIER DE LA S.D.E. MAIL ?
TEST.MAIL
-- NOM DU FICHIER DE LA S.D.S. BDCL ?
TEST.BDCL
-- IL Y A DES TABLEAUX A ASSOCIER (OUI-NON) ?
N
-- LES VALEURS DE BLOCAGES SONT :
1 ==> CONSTANTES , 2 ==> DONNEES PAR FONCTION ?
2
-- TYPE DES VALEURS A BLOQUER : 2 (SIMPLE) 5 (DOUBLE PRECISION) ?
2
-- VOULEZ-VOUS RESTAURER LA S.D.E. MAIL POUR VOUS GUIDER (OUI-NON) ?
OUI
-- BLOQUER DES D.L. SUR LA REFERENCE 1 (OUI-NON) ?
O
-- BLOQUER L'INCONNUE VARIATIONNELLE : TEMPERATURE (OUI-NON) ?
O
** BLOCAGE DE SON MNEMONIQUE : VN
-- BLOQUER DES D.L. SUR LA REFERENCE 2 (OUI-NON) ?
O
-- BLOQUER L'INCONNUE VARIATIONNELLE : TEMPERATURE (OUI-NON) ?
O
** BLOCAGE DE SON MNEMONIQUE : VN
-- UTILISEZ-VOUS LES FONCTIONS INTERPRETEES (OUI-NON) ?
O
-- NOM DU FICHIER DE LA S.D.E. COOR ?
TEST.COOR
-- UTILISEZ VOUS LES COORDONNEES DE POINTS NON SOMMETS (OUI-NON) ?
O
** DONNER L'EXPRESSION VALCLR(X,Y,Z) EN FINISSANT PAR ;
POUR LA FRONTIERE 1 POUR SON INCONNUE 1 POUR SON MNEMONIQUE VN
** EXEMPLE :' X**2 + Y -1;'
OU : X**2+Y-1;
0.;
** DONNER L'EXPRESSION VALCLR(X,Y,Z) EN FINISSANT PAR ;
POUR LA FRONTIERE 2 POUR SON INCONNUE 1 POUR SON MNEMONIQUE VN
(X-X*X*X)*(Y-Y*Y*Y);
-- LE NOMBRE DE DL PAR NOEUD EST CONSTANT (OUI-NON) ?
O
-- CONDITIONS EN RELATION LINEAIRE :
0 PAS DE CONDITIONS
1 ENTREE A LA MAIN ( < 20 )
-1 ENTREE PAR S.P. SPCLRL
0
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
E
-- NOM DU FICHIER CONTENANT LES DONNEES ?
BDCL.DATA
-- PARAMETRE D'IMPRESSION DE LA SD ?
1
++ OPEN(11,FILE='test.mail',SPEC='OLD,UNFORMATTED',RECL=0)
++ OPEN(12,FILE='test.bdcl',SPEC='UNFORMATTED',RECL=0)
++ OPEN(13,FILE='test.coor',SPEC='OLD,UNFORMATTED',RECL=0)
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE CORNOE :
FIN DU MODULE CORNOE
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE COBDC1 :
FIN DU MODULE COBDC1
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
TABLEAU B D C 2
----------------
TYPE DES VALEURS DE BLOCAGE (NTYB) : 2
NOMBRE DE CARTES DECRIVANT LES BLOCAGES (NCART) : 52
NOMBRE DE RELATIONS LINEAIRES DE BLOCAGE (NCLRL) : 0
NUMERO D'OPTION DE STOCKAGE (NOPTFI) : 0
NOMBRE DE MOTS DU TABLEAU BDC3 (NMMAT3) : 156
NOMBRE DE MOTS DU TABLEAU BDC4 (NMMAT4) : 52
NOMBRE DE MOTS DU TABLEAU BDC5 (NMMAT5) : 0
NOMBRE DE MOTS DU TABLEAU BDC6 (NMMAT6) : 0
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
FIN
Le fichier de données produit est le suivant:
TEST.MAIL $ NOM DU FICHIER
35 $ ET NIVEAU DE LA SD MAIL
TEST.BDCL $ NOM DU FICHIER
35 $ ET NIVEAU DE LA SD BDCL
0 $ NTBDCL
2 2 2 $ ICONST NBFR NTYP
1 1 VN $ REF INC.VARIATIONNELLE MNEMO
2 1 VN $ REF INC.VARIATIONNELLE MNEMO
1 $ 1 SI FONCTIONS INTERPRETEES
TEST.COOR $ NOM DU FICHIER
35 $ ET NIVEAU DE LA SD COOR
1 $ 1 SI SD COOR DES NOEUDS
2 $ NOMBRE DE FONCTIONS
VALCLR01(X,Y,Z)=
0.;
VALCLR02(X,Y,Z)=
(X-X*X*X)*(Y-Y*Y*Y);
FIN
0 $ 1 SI SD NDL1
0 $ 1 SI CL EN RL A LA MAIN ;
$ -1 SI CL EN RL PAR SP
Les conditions aux limites étant connues, la solution est calculée en utilisant le préprocesseur CHOLXX. On construit d'abord un fichier de données en prenant l'option CREATION du menu principal.
Les données demandées sont les suivantes:
le nom du fichier contenant cette S.D. BDCL (ex: TEST.BDCL).
Il n'y a pas de relations linéaires (ex: N).
On active CHOLXX en prenant l'option EXECUTION du menu principal.
Les données utiles sont alors:
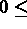IMPRE 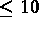) (ex: 5).
On montre ci-dessous la session obtenue en exécutant le
préprocesseur
[4] CHOLXX:
B$ cholxx
******************************************
APPEL DE LA RESOLUTION METHODE DE CHOLESKY
******************************************
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
C
*******************************************************************************
CREATION CONVERSATIONNELLE DES DONNEES DE L'ENCHAINEMENT CHOLESKY (SEQUENTIEL)
*******************************************************************************
-- NOM DU FICHIER DE DONNEES A CREER ?
B.DATA
-- NOM DU FICHIER DE LA S.D.E. MAIL ?
TEST.MAIL
-- NOMBRE DE CAS DE CHARGE (NDSM) ?
TYPE DES VALEURS DU PROBLEME (NTYP) ?
1 2
-- LE NOMBRE DE DL PAR NOEUD EST IL CONSTANT (OUI-NON) ?
O
-- NOMBRE DE DL PAR NOEUD ?
1
-- NOM DU FICHIER DE LA S.D.E. TAE ?
TEST.TAE
-- Y A T'IL DES CONDITIONS AUX LIMITES FORCEES (OUI-NON) ?
O
-- NOM DU FICHIER DE LA S.D.E. BDCL ?
TEST.BDCL
-- Y A T'IL DES RELATIONS LINEAIRES (OUI-NON) ?
N
-- NOM DU FICHIER DE LA S.D.S. B ?
TEST.B
-- PARAMETRE D'IMPRESSION DE LA SOLUTION ?
6
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
E
-- NOM DU FICHIER CONTENANT LES DONNEES ?
B.DATA
-- PARAMETRE D'IMPRESSION POUR L'EXECUTION ?
1
++ OPEN(11,FILE='test.mail',SPEC='OLD,UNFORMATTED',RECL=0)
++ OPEN(12,FILE='test.tae',SPEC='OLD,UNFORMATTED',RECL=0)
++ OPEN(13,FILE='test.bdcl',SPEC='OLD,UNFORMATTED',RECL=0)
++ OPEN(14,FILE='test.b',SPEC='UNFORMATTED',RECL=0)
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE PREPAC :
NOMBRE DE MOTS DE LA MATRICE (LMUA5) : 1998
DIFFERENCE MAX ENTRE 2 NOEUDS D'UN ELEMENT (LBDP) : 30
DIFFERENCE MAX ENTRE 2 D.L. D'UN ELEMENT (LBDPDL) : 30
NOMBRE MAX DE NOEUDS D'UN ELEMENT (NNOMAX) : 6
NOMBRE DE SECONDS MEMBRES (NDSM) : 1
NOMBRE DE MOTS EN M.C. POUR LA S.D. NDL1 (MCNDL1) : 0
NOMBRE DE MOTS EN M.C. POUR LA S.D. MUA (MCMUA) : 2216
NOMBRE DE MOTS EN M.C. POUR LA S.D. B (MCB) : 216
FIN DU MODULE PREPAC
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE ASSMUA :
FIN DU MODULE ASSMUA
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE ASEMBV :
FIN DU MODULE ASEMBV
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
FIN DU MODULE CLIMPC
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE CHOLPC :
FIN DU MODULE CHOLPC
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE DRCHPC :
FIN DU MODULE DRCHPC
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
IMPRESSION DE LA S.D. B DE NIVEAU 1
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
TITRE :
DATE ET NOM UTILISATEUR : 04/04/91 george
TYPE DE LA STRUCTURE DE DONNEES : B
NIVEAU ET NUMERO D'ETAT : 1 2
NOMBRE DE TABLEAUX ASSOCIES : 0
TABLEAU B 2
------------
TYPE DU TABLEAU (NTYT) : 2
NOMBRE DE SES INDICES ET LEURS MAXI (NIND..) : 2 1 171
TRAITEMENT (1:PAGES DE MEME TAILLE,0:SINON) (NCOD) : 1
NOMBRE DE PAGES DU TABLEAU B4 (NBLOC) : 1
NOMBRE DE NOEUDS (NOE) : 171
NOMBRE DE TABLEAUX B4 DANS CETTE S.D. (NBBLOC) : 1
NOMBRE CONSTANT DE D.L. PAR NOEUD OU 0 (ND) : 1
NOMBRE DE D.L. OU LONGUEUR D'UNE PAGE DE B4 (NTDL) : 171
CODE DE STOCKAGE DE B (NCODSB) : -1
TABLEAU B 3
------------
POINTEUR SUR LA DERNIERE LIGNE DE CHAQUE PAGE DE B
1 0 2 171
TABLEAU B4(NDSM,NTDL) NUMERO : 1
-------------------------------------
TABLEAU B4(NDSM,NTDL) PAGINE EN 1 OU PLUSIEURS PAGES
----------------------------------------------------
PAGE 1
----------
------------------------------------------------------
| NOEUD | DL | DL GLOBAL | LE (LES) CAS DE CHARGE |
------------------------------------------------------
| 1 | 1 | 1 | 0.395995E-01
| 2 | 1 | 2 | 0.000000
| 3 | 1 | 3 | 0.633240E-01
| 4 | 1 | 4 | 0.000000
| 5 | 1 | 5 | 0.000000
| 6 | 1 | 6 | 0.000000
| 7 | 1 | 7 | 0.000000
| 8 | 1 | 8 | 0.000000
| 9 | 1 | 9 | 0.733094E-01
| 10 | 1 | 10 | 0.739653E-01
-- CREATION DU DATA =-= EXECUTION MODULE (DATA EXISTANT) =-= FIN =-= ?
- - -
FIN
Le fichier de données construit est le suivant:
TEST.MAIL $ NOM DU FICHIER
1 $ ET NIVEAU DE LA SD MAIL
1 2 1 $ NDSM NTYP ND
TEST.TAE $ NOM DU FICHIER
1 $ ET NIVEAU DE LA SD TAE
1 $ 1 SI BDCL EST UTILISE , 0 SINON
TEST.BDCL $ NOM DU FICHIER
1 $ ET NIVEAU DE LA SD BDCL
0 $ 1 SI CL. EN RL. EXISTE
TEST.B $ NOM DU FICHIER
1 $ ET NIVEAU DE LA SD B
6 $ IMPREB
Si la solution exacte du problème est connue, on peut utiliser le post-processeur NORMXX pour déterminer la précision de la solution numérique en calculant des normes d'erreurs.
Les données de ce processeur sont les suivantes:
On décrit alors les informations suivantes:
La session apparaissant à l'écran est montrée ci-dessous:
B$ normxx
**************
APPEL DE NORME : ( TEST AVEC SOLUTION EXACTE )
**************
-- FINIR : 0 ?
-- NORME RELATIVE A UNE S.D.E B : 1 ?
-- " " A UNE S.D.E TAE : 2 ?
-- (CONTRAINTES)
-- NORME ENERGIE : 3 ?
1
-- NOM DU FICHIER DE LA S.D.E. MAIL ?
TEST.MAIL
-- NOM DU FICHIER DE LA S.D.E. COOR ?
TEST.COOR
-- NOM DU FICHIER DE LA S.D.E. B (SOLUTION) ?
%% LA SDB DOIT ETRE EN ACCES SEQUENTIEL
TEST.B
-- VOULEZ VOUS STOKER L'ERREUR (OUI - NON) ?
N
-- PARAMETRE D'IMPRESSION ?
6
-- VOULEZ-VOUS UTILISER LES FONCTIONS INTERPRETEES (OUI-NON) ?
O
-- NOM DU FICHIER DESCRIPTIF DES FONCTIONS INTERPRETEES
SOLUTION
++ OPEN(37,FILE='solution',SPEC='',RECL=0)
-- CE FICHIER EXISTE DEJA (OUI-NON) ?
N
-- NOMBRE DE DEGRE DE LIBERTE A DECRIRE ?
1
-- TYPE DE LA SOLUTION ( 2 EN SIMPLE PRECISION , 5 EN DOUBLE ) ?
2
** DONNER L'EXPRESSION SOLEX(X,Y,Z) EN FINISSANT PAR ;
POUR LE DEGRE DE LIBERTE : 1
** EXEMPLE :' X**2 + Y -1;'
OU : X**2+Y-1;
(X-X**3.)*(Y-Y**3.);
-- SORTIE SUR ECRAN (OUI-NON) ?
OUI
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE NORME :
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
-------------------------------------------------------------------------
| NOEUD | DL | DL GLOBAL | MNEMO | SOL EXACTE | SOL CALCULEE | % |
-------------------------------------------------------------------------
| 1 | 1 | 1 | VN | 0.39400E-01 0.39599E-01 | 101. |
| 2 | 1 | 2 | VN | 0.00000E+00 0.00000E+00 | 100. |
| 3 | 1 | 3 | VN | 0.63040E-01 0.63324E-01 | 100. |
| 4 | 1 | 4 | VN | 0.00000E+00 0.00000E+00 | 100. |
| 5 | 1 | 5 | VN | 0.00000E+00 0.00000E+00 | 100. |
| 6 | 1 | 6 | VN | 0.00000E+00 0.00000E+00 | 100. |
| 7 | 1 | 7 | VN | 0.00000E+00 0.00000E+00 | 100. |
| 8 | 1 | 8 | VN | 0.00000E+00 0.00000E+00 | 100. |
| 9 | 1 | 9 | VN | 0.73171E-01 0.73309E-01 | 100. |
.
.
.
| 171 | 1 | 171 | VN | 0.00000E+00 0.00000E+00 | 100. |
-------------------------------------------------------------------------
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
IMPRESSION DE LA S.D. MAIL DE NIVEAU 0
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
TITRE :
DATE ET NOM UTILISATEUR : 04/04/91 george
TYPE DE LA STRUCTURE DE DONNEES : MAIL
NIVEAU ET NUMERO D'ETAT : 0 0
NOMBRE DE TABLEAUX ASSOCIES : 0
TABLEAU M A I 2
----------------
DIMENSION DE L'ESPACE (NDIM) : 2
NOMBRE D'INCONNUES DE LA FORMULATION VARIATIONNELLE (NINCFV) : 1
NOMBRE DE TYPES D'ELEMENTS (NTYELM) : 2
NOMBRE DE NUMEROS DE REFERENCES (NNR) : 2
NOMBRE DE TYPES DE NOEUDS (NTYNOE) : 1
NOMBRE DE TYPES DE POINTS (NTYPOI) : 1
NOMBRE DE MOTS DU TABLEAU MAI3 (LMAI3) : 36
LES POINTS NE SONT DEFINIS QUE PAR LEURS COORDONNEES
NOEUDS ET POINTS NE COINCIDENT PAS PARTOUT (NCO) : 0
NOMBRE MAXIMUM DE MOTS POUR UN ELEMENT (NMMAEL) : 28
NOMBRE DE MOTS DU TABLEAU MAIL (LMAIL) : 1421
OPTION DE STOCKAGE (NOPFI) : 0
TABLEAU M A I 3
----------------
NOMBRE D'ELEMENTS (NE) : 72
NOMBRE DE NOEUDS (NOE) : 171
NOMBRE DE POINTS (NP) : 65
NOMBRE DE SOUS-DOMAINES (NDSD) : 1
*** TABLEAU DES TYPES D'ELEMENTS ***
--------------------------------------------------------------------------------
| S-D | NOEUD | SEGMENT | TRIANGLE | QUADRANGLE |
--------------------------------------------------------------------------------
| | DROIT COURBE | DROIT COURBE | DROIT COURBE | DROIT COURBE |
--------------------------------------------------------------------------------
| 1 | | | | |TRIA2P2D|TRIA2P2C| | |
--------------------------------------------------------------------------------
--------------------------------------------------------------------------------
| S-D | TETRAEDRE | PENTAEDRE | HEXAEDRE | SUPER-ELEMENT |
--------------------------------------------------------------------------------
| | DROIT COURBE | DROIT COURBE | DROIT COURBE | DROIT COURBE |
--------------------------------------------------------------------------------
| 1 | | | | | | | | |
--------------------------------------------------------------------------------
TABLEAUX M A I 5 A M A I 8
-------------------------------
DESCRIPTION DES TYPES DE NOEUDS
NOMBRE D'INCONNUES VARIATIONNELLES DE CHAQUE TYPE DE NOEUD
----------------------------------------------------------
TYPE 1 : 1
TYPE DE NOEUD 1 :
--------------------
TEMPERATURE (INCONNUE : 1) : VN
TABLEAUX M A I B A M A I K
-------------------------------
DESCRIPTION DES TYPES D'ELEMENTS
TYPE D'ELEMENT 1 :
-------------------
NOM DE L'ELEMENT : THERTRIA2P2D
CODE DE L'ELEMENT : 100002
L'ELEMENT EST UN : TRIANGLE
NOMBRE DE NOEUDS : 6
NOMBRE DE POINTS : 3
NOMBRE DE TABLEAUX ASSOCIES : 1
-------------------------------------------------------------------------------
| NOEUD | TYPE | COORDONNEES SUR L'ELEMENT UNITE |
-------------------------------------------------------------------------------
| 1 | 1 | 0.0000000 0.0000000
| 2 | 1 | 1.000000 0.0000000
| 3 | 1 | 0.0000000 1.000000
| 4 | 1 | 0.5000000 0.0000000
| 5 | 1 | 0.5000000 0.5000000
| 6 | 1 | 0.0000000 0.5000000
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
| POINT | TYPE | COORDONNEES SUR L'ELEMENT UNITE |
-------------------------------------------------------------------------------
| 1 | 1 | 0.0000000 0.0000000
| 2 | 1 | 1.000000 0.0000000
| 3 | 1 | 0.0000000 1.000000
-------------------------------------------------------------------------------
TABLEAU 1 ( TYPE ENTIER ) : 1 INDICE(S) DE VALEUR MAXI : 7
TYPE D'ELEMENT 2 :
-------------------
NOM DE L'ELEMENT : THERTRIA2P2C
CODE DE L'ELEMENT : 100003
L'ELEMENT EST UN : TRIANGLE
NOMBRE DE NOEUDS : 6
NOMBRE DE POINTS : 6
NOMBRE DE TABLEAUX ASSOCIES : 1
-------------------------------------------------------------------------------
| NOEUD | TYPE | COORDONNEES SUR L'ELEMENT UNITE |
-------------------------------------------------------------------------------
| 1 | 1 | 0.0000000 0.0000000
| 2 | 1 | 1.000000 0.0000000
| 3 | 1 | 0.0000000 1.000000
| 4 | 1 | 0.5000000 0.0000000
| 5 | 1 | 0.5000000 0.5000000
| 6 | 1 | 0.0000000 0.5000000
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
| POINT | TYPE | COORDONNEES SUR L'ELEMENT UNITE |
-------------------------------------------------------------------------------
| 1 | 1 | 0.0000000 0.0000000
| 2 | 1 | 1.000000 0.0000000
| 3 | 1 | 0.0000000 1.000000
| 4 | 1 | 0.5000000 0.0000000
| 5 | 1 | 0.5000000 0.5000000
| 6 | 1 | 0.0000000 0.5000000
-------------------------------------------------------------------------------
TABLEAU 1 ( TYPE ENTIER ) : 1 INDICE(S) DE VALEUR MAXI : 7
DL ERREUR ERREUR NORME ERREUR ERREUR AU NOEUD
ABSOLUE L2 RELATIVE L2 L2 SOLUTION RELATIVE L1 MAXIMUM
1 0.39979E-02 0.41671E-02 0.95940E+00 0.46747E-02 0.21464E+00 67
X = 0.934672 Y = -0.921138E-03
-- FINIR : 0 ?
-- NORME RELATIVE A UNE S.D.E B : 1 ?
-- " " A UNE S.D.E TAE : 2 ?
-- (CONTRAINTES)
-- NORME ENERGIE : 3 ?
0
Les résultats sont dessinés en utilisant le préprocesseur TRMCXX. La figure 4.3 est obtenue en appelant TRMCXX et en donnant les noms des fichiers des S.D. MAIL et COOR. Les isovaleurs sont dessinées par le même préprocesseur, en prenant l'option adéquate du menu et en donnant le nom du fichier contenant la S.D. B. Le résultat est visible sur la figure 4.4.
Commentaire: Noter la différence entre les dessins obtenus via TRNOXX et via TRMCXX, ce dernier utilisant le fait que l'interpolation est connue.
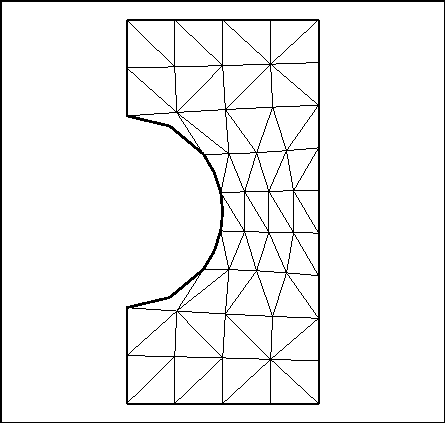
Figure: Maillage (dessin dû à TRMCXX)
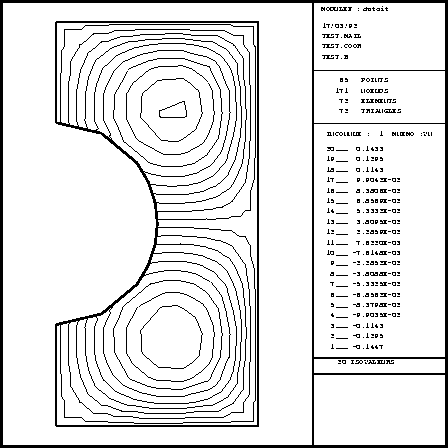
Figure: Isovaleurs (dessin dû à TRMCXX)